Dieser Begriff hat andere Bedeutungen, siehe Interpolation. Zur Funktion siehe: Interpolant.

Interpolation, Interpolation (aus lat. interpolis - « geglättet, erneuert, erneuert; umgewandelt"") - in der Computermathematik eine Methode zum Finden von Zwischenwerten einer Größe aus einem vorhandenen diskreten Satz bekannter Werte. Der Begriff "Interpolation" wurde erstmals von John Vallis in seiner Abhandlung The Arithmetic of the Infinite (1656) verwendet.

In der Funktionsanalyse ist die Interpolation linearer Operatoren ein Abschnitt, der Banachräume als Elemente einer bestimmten Kategorie betrachtet.

Viele, die sich mit naturwissenschaftlichen und ingenieurwissenschaftlichen Berechnungen befassen, müssen oft mit empirisch oder durch Stichproben gewonnenen Wertemengen arbeiten. In der Regel ist es erforderlich, auf der Grundlage dieser Mengen eine Funktion zu konstruieren, auf der man könnte hohe Präzision um andere empfangene Werte zu erhalten. Eine solche Aufgabe wird Approximation genannt. Interpolation ist eine Art Näherung, bei der die Kurve der konstruierten Funktion genau durch die verfügbaren Datenpunkte verläuft.

Es gibt auch ein Problem in der Nähe der Interpolation, das darin besteht, eine komplexe Funktion durch eine andere, einfachere Funktion zu approximieren. Wenn eine bestimmte Funktion für produktive Berechnungen zu komplex ist, können Sie versuchen, ihren Wert an mehreren Stellen zu berechnen und daraus mehr aufzubauen, dh zu interpolieren eine einfache Funktion. Die Verwendung einer vereinfachten Funktion erlaubt es Ihnen natürlich nicht, dieselben genauen Ergebnisse zu erhalten, die die ursprüngliche Funktion liefern würde. Aber bei einigen Klassen von Problemen kann der Gewinn an Einfachheit und Geschwindigkeit der Berechnungen den daraus resultierenden Fehler in den Ergebnissen aufwiegen.

Wir sollten auch eine ganz andere Art der mathematischen Interpolation erwähnen, die als "Operatorinterpolation" bekannt ist. Zu den klassischen Arbeiten zur Operatorinterpolation gehören das Riesz-Thorin-Theorem und das Marcinkiewicz-Theorem, die die Grundlage für viele andere Arbeiten bilden.

Definitionen

Betrachten Sie ein System nicht übereinstimmender Punkte x i (\displaystyle x_(i)) (i ∈ 0 , 1 , … , N (\displaystyle i\in (0,1,\dots ,N))) aus einem Bereich D ( \displaystyle D) . Die Werte der Funktion f (\displaystyle f) seien nur an diesen Stellen bekannt:

Y ich = f (x ich) , ich = 1 , … , N . (\displaystyle y_(i)=f(x_(i)),\quad i=1,\ldots ,N.)

Das Problem der Interpolation besteht darin, eine Funktion F (\displaystyle F) aus einer gegebenen Klasse von Funktionen zu finden, so dass

F (x ich) = y ich , ich = 1 , … , N . (\displaystyle F(x_(i))=y_(i),\quad i=1,\ldots ,N.)

• Die Punkte x i (\displaystyle x_(i)) werden aufgerufen Interpolationsknoten, und ihre Gesamtheit ist Interpolationsgitter.
• Paare (x i , y i) (\displaystyle (x_(i),y_(i))) werden aufgerufen Datenpunkte oder Basispunkte.
• Unterschied zwischen "benachbarten" Werten ​​Δ x i = x i − x i − 1 (\displaystyle \Delta x_(i)=x_(i)-x_(i-1)) - Interpolationsgitterschritt. Sie kann sowohl variabel als auch konstant sein.
• Funktion F (x) (\displaystyle F(x)) - interpolierende Funktion oder Interpolant.

Beispiel

1. Nehmen wir an, wir haben eine Tabellenfunktion wie die folgende, die für mehrere Werte von x (\displaystyle x) die entsprechenden Werte von f (\displaystyle f) bestimmt:

X (\displaystyle x) f (x) (\displaystyle f(x))

0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

Die Interpolation hilft uns zu wissen, welchen Wert eine solche Funktion an einem anderen als den angegebenen Punkten haben kann (z. B. wann x = 2,5).

Bis heute gibt es viele verschiedene Wege Interpolation. Die Wahl des am besten geeigneten Algorithmus hängt von den Antworten auf die Fragen ab: Wie genau ist die gewählte Methode, was kostet ihre Anwendung, wie glatt ist die Interpolationsfunktion, wie viele Datenpunkte benötigt sie usw.

2. Finden Sie einen Zwischenwert (mit lineare Interpolation).

6000	15.5
6378	?
8000	19.2

15,5 + (6378 − 6000) 8000 − 6000 ∗ (19,2 − 15,5) 1 = 16,1993 (\displaystyle ?=15,5+(\frac ((6378-6000))(8000-6000))*(\frac ((19,2- 15.5))(1))=16.1993)

Bei Programmiersprachen

Ein Beispiel für lineare Interpolation für die Funktion y = 3 x + x 2 (\displaystyle y=3x+x^(2)) . Der Benutzer kann eine Zahl zwischen 1 und 10 eingeben.

Fortran

program interpol integer i real x, y, xv, yv, yv2 dimension x(10) dimension y(10) call prisv(x, i) call func(x, y, i) write(*,*) "Zahl eingeben: " read(*,*) xv if ((xv >= 1).and.(xv xv)) then yv2 = ((xv - x(i)) * (y(i+1) - y(i)) / (x(i+1) - x(i))) + y(i) end if end do end subroutine

C++

int main() ( system("COLOR 0A"); double ob, x1, x2, y1, y2, p1, p2, pi, skolko, status; system("echo Interpolate X1 - X2 "); system("echo Enter number: "); cin >> ob; system("echo Zum Beispiel 62, C1 = 60, L1 = 1,31, C2 = 80, L2 = 1,29"); cout > x1; cout > x2; cout > y1; cout > y2 ; p1 = y1 - x1; p2 = y2 - x2; pi = p2 / p1; skolko = ob - x1; status = x2 + (pi * skolko); cout

Interpolationsmethoden

Nächste-Nachbar-Interpolation

Das einfachste Interpolationsverfahren ist die Nächste-Nachbar-Interpolation.

Interpolation durch Polynome

In der Praxis wird am häufigsten die Interpolation durch Polynome verwendet. Dies liegt hauptsächlich daran, dass Polynome leicht zu berechnen sind, ihre Ableitungen leicht analytisch gefunden werden können und die Menge der Polynome im Raum stetiger Funktionen dicht ist (Satz von Weierstraß).

• Lineare Interpolation
• Newtons Interpolationsformel
• Finite-Differenzen-Methode
• IMN-1 und IMN-2
• Lagrange-Polynom (Interpolationspolynom)
• Aitkens Schema
• Spline-Funktion
• kubischer Spline

Rückwärtsinterpolation (Berechnung von x bei y)

• Lagrange-Polynom
• Inverse Interpolation nach Newtons Formel
• Inverse Gauß-Interpolation

Multivariable Funktionsinterpolation

• Bilineare Interpolation
• Bikubische Interpolation

Andere Interpolationsmethoden

• Rationale Interpolation
• Trigonometrische Interpolation

Verwandte konzepte

• Extrapolation - Methoden zum Finden von Punkten außerhalb eines bestimmten Intervalls (Kurvenverlängerung)
• Annäherung - Methoden zum Erstellen von Annäherungskurven

Umgekehrte Interpolation

auf der Klasse der Funktionen aus dem Raum C2, deren Graphen durch die Punkte des Arrays (xi, yi) gehen, i = 0, 1, . . . , m.

Lösung. Unter allen Funktionen, die durch die Bezugspunkte (xi, f(xi)) gehen und zu dem genannten Raum gehören, ist es der kubische Spline S(x), der die Randbedingungen S00(a) = S00(b) = 0 erfüllt die das Extremum (Minimum) der Funktion I(f) liefert.

In der Praxis besteht oft das Problem, den gegebenen Wert der Funktion des Argumentwerts zu suchen. Dieses Problem wird durch umgekehrte Interpolationsverfahren gelöst. Wenn die gegebene Funktion monoton ist, besteht die einfachste Möglichkeit zur Durchführung einer Rückwärtsinterpolation darin, die Funktion durch ein Argument zu ersetzen und umgekehrt und dann zu interpolieren. Wenn die gegebene Funktion nicht monoton ist, kann diese Technik nicht verwendet werden. Dann schreiben wir, ohne die Rollen der Funktion und des Arguments zu ändern, diese oder jene Interpolationsformel auf; unter Verwendung der bekannten Werte des Arguments und unter der Annahme, dass die Funktion bekannt ist, lösen wir die resultierende Gleichung in Bezug auf das Argument.

Die Schätzung des Restterms bei der ersten Methode ist dieselbe wie bei der direkten Interpolation, nur müssen die Ableitungen der direkten Funktion durch Ableitungen der inversen Funktion ersetzt werden. Schätzen wir den Fehler der zweiten Methode ab. Wenn uns eine Funktion f(x) gegeben ist und Ln (x) das Lagrange-Interpolationspolynom ist, das für diese Funktion über den Knoten x0, x1, x2, . . . , xn, dann

f (x) − Ln (x) = (n + 1)! (x − x0) . . . (x − xn) .

Angenommen, wir müssen einen Wert x¯ finden, so dass f (¯x) = y¯ (y¯ ist gegeben). Wir lösen die Gleichung Ln (x) = y¯ . Lass uns einen Wert x¯ bekommen. Durch Einsetzen in die vorherige Gleichung erhalten wir:

Mn+1

f (x¯) − Ln (x¯) = f (x¯) − y¯ = f (x¯) − f (¯x) =
Wenden wir die Langrange-Formel an, erhalten wir
(x¯ − x¯) f0 (η) =
wobei η zwischen x¯ und x¯ liegt. Wenn ein Intervall ist, das x¯ und x¯ und min enthält

aus dem letzten Ausdruck folgt:

|x¯ − x¯| 6m1(n + 1)! |$n (x¯)| .

In diesem Fall wird natürlich vorausgesetzt, dass wir die Gleichung Ln (x) = y¯ exakt gelöst haben.

Verwenden der Interpolation für die Tabellierung

Die Theorie der Interpolation findet Anwendung bei der Erstellung von Funktionstabellen. Nachdem der Mathematiker ein solches Problem erhalten hat, muss er eine Reihe von Fragen lösen, bevor er mit den Berechnungen beginnt. Die Formel, nach der die Berechnungen durchgeführt werden, muss ausgewählt werden. Diese Formel kann von Standort zu Standort variieren. Normalerweise sind Formeln zur Berechnung von Funktionswerten umständlich und werden daher verwendet, um einige Referenzwerte zu erhalten, und verdicken dann durch Subtabellierung die Tabelle. Die Formel, die gibt Referenzwerte Funktion, sollte die erforderliche Genauigkeit der Tabellen unter Berücksichtigung der folgenden Untertabellen liefern. Wenn Sie Tabellen mit einer konstanten Schrittweite kompilieren möchten, müssen Sie zuerst deren Schrittweite bestimmen.

Zurück Erster Voriger Nächster Letzter Index überspringen

Am häufigsten werden Funktionstabellen so erstellt, dass eine lineare Interpolation (d. h. eine Interpolation unter Verwendung der ersten beiden Terme der Taylor-Formel) möglich ist. In diesem Fall sieht der Restterm so aus

R1 (x) = f00 (ξ)h2t(t − 1).

Hier gehört ξ zum Intervall zwischen zwei benachbarten Tabellenwerten des Arguments, in dem sich x befindet, und t zwischen 0 und 1 liegt. Das Produkt t(t − 1) nimmt den größten Modulo an

Wert bei t = 12. Dieser Wert ist gleich 14. So,

Es muss daran erinnert werden, dass neben diesem Fehler - dem Fehler der Methode - bei der praktischen Berechnung von Zwischenwerten noch ein nicht behebbarer Fehler und Rundungsfehler auftritt. Wie wir bereits gesehen haben, ist der schwerwiegende Fehler bei der linearen Interpolation gleich dem Fehler der tabellierten Werte der Funktion. Der Rundungsfehler hängt von den Rechenmitteln und vom Berechnungsprogramm ab.

Zurück Erster Voriger Nächster Letzter Index überspringen

Subject Index

geteilte Differenzen zweiter Ordnung, 8 erster Ordnung, 8

Keil, 15

Stützstellen, 4

Zurück Erster Voriger Nächster Letzter Index überspringen

/ Material_studentam_po_RGR_BZhD / Wie man interpoliert

Formel zur Interpolation von Tabellendaten

Wird im 2. Schritt verwendet, wenn der Betrag von NXR (Q, t) aus der Bedingung stammt liegt dazwischen 100 t und 300 t.

(Ausnahme: wenn Q bedingt gleich 100 oder 300 ist, dann ist keine Interpolation erforderlich).

j Ö- Ihre anfängliche NHR-Menge aus der Bedingung in Tonnen

(entspricht dem Buchstaben Q)

j 1 – kleiner

(aus den Tabellen 11-16, normalerweise 100).

j 2 – mehr am nächsten zu Ihrem Wert der Menge an NCR, in Tonnen

(aus den Tabellen 11-16, normalerweise 300).

x 1 j 1 (x 1 gegenüber gelegen j 1 ), km.

x 2 - Tabellenwert der Ausbreitungstiefe einer Wolke kontaminierter Luft (G t). j 2 (x 2 gegenüber gelegen j 2 ), km.

x 0 - gewünschter Wert G t dazugehörigen j Ö(laut Formel).

Beispiel.

NCR - Chlor; Q = 120 t;

Art des SVSP (Grad des vertikalen Luftwiderstands) - Inversion.

Finden G t- Tabellenwert der Ausbreitungstiefe der Wolke kontaminierter Luft.

Wir sehen die Tabellen 11-16 durch und finden Daten, die zu Ihrem Zustand passen (Chlor, Inversion).

Passender Tisch 11.

Werte auswählen j 1 , j 2, x 1 , x 2 . Wichtig - Wir nehmen die Windgeschwindigkeit 1 m / s. Wir nehmen die Temperatur - 20 ° C.

Ersetzen Sie die ausgewählten Werte in der Formel und finden Sie x 0 .

Wichtig - Berechnung ist richtig, wenn x 0 wird einen Wert irgendwo dazwischen haben x 1 , x 2 .

1.4. Lagrange-Interpolationsformel

Der von Lagrange vorgeschlagene Algorithmus zur Konstruktion der Interpolation

Funktionen nach Tabellen (1) sieht die Konstruktion des Interpolationspolynoms Ln(x) in der Form vor

Offensichtlich bestimmt die Erfüllung der Bedingungen (11) für (10) die Erfüllung der Bedingungen (2) der Formulierung des Interpolationsproblems.

Die Polynome li(x) werden wie folgt geschrieben

Beachten Sie, dass kein einziger Faktor im Nenner der Formel (14) gleich Null ist. Nachdem Sie die Werte der Konstanten ci berechnet haben, können Sie sie verwenden, um die Werte der interpolierten Funktion an bestimmten Punkten zu berechnen.

Die Lagrange-Interpolationspolynomformel (11) kann unter Berücksichtigung der Formeln (13) und (14) geschrieben werden als

qi (x − x0)(x − x1) K (x − xi −1)(x − xi +1) K (x − xn)

1.4.1. Organisation der manuellen Berechnungen nach der Lagrange-Formel

Die direkte Anwendung der Lagrange-Formel führt zu einer Vielzahl gleichartiger Berechnungen. Für Tische mit kleinen Abmessungen können diese Berechnungen sowohl manuell als auch in der Softwareumgebung durchgeführt werden.

In der ersten Phase betrachten wir den Algorithmus der manuell durchgeführten Berechnungen. In Zukunft sollen die gleichen Berechnungen in der Umgebung wiederholt werden

Microsoft Excel oder OpenOffice.org Calc.

Auf Abb. 6 zeigt ein Beispiel der Quellentabelle einer interpolierten Funktion, die durch vier Knoten definiert ist.

Abb.6. Tabelle mit den Anfangsdaten für die vier Knoten der interpolierten Funktion

In die dritte Spalte der Tabelle schreiben wir die Werte der Koeffizienten qi, die nach Formeln (14) berechnet wurden. Nachfolgend finden Sie eine Aufzeichnung dieser Formeln für n = 3.

q0=Y0/(x0-x1)/(x0-x2)/(x0-x3)q1=Y1/(x1-x0)/(x1-x2)/(x1-x3)(16) q2=Y2/( x2-x0)/(x2-x1)/(x2-x3)q3=Y3/(x3-x0)/(x3-x1)/(x3-x2)

Der nächste Schritt bei der Implementierung manueller Berechnungen ist die Berechnung der Werte li(x) (j=0,1,2,3), durchgeführt durch Formeln (13).

Lassen Sie uns diese Formeln für die Version der Tabelle schreiben, die wir mit vier Knoten betrachten:

l0(x)=q0(x-x1) (x-x2) (x-x3),

l1(x)=q1(x-x0) (x-x2) (x-x3),

l2(x)=q2(x-x0)(x-x1)(x-x3),(17) l3(x)=q3(x-x0)(x-x1)(x-x2) .

Lassen Sie uns die Werte der Polynome li(xj) (j=0,1,2,3) berechnen und in die Zellen der Tabelle eintragen. Die Werte der Funktion Ycalc(x) gemäß Formel (11) werden als Ergebnis der Summierung der Werte von li(xj) in Zeilen erhalten.

Das Format der Tabelle, die Spalten mit berechneten Werten li(xj) und eine Spalte mit Werten Ycalc(x) enthält, ist in Abb. 8 dargestellt.

Reis. 8. Tabelle mit den Ergebnissen der manuellen Berechnungen, die mit den Formeln (16), (17) und (11) für alle Werte des Arguments xi durchgeführt wurden

Nachdem die Bildung der Tabelle in Abb. 8, durch die Formeln (17) und (11) ist es möglich, den Wert der interpolierten Funktion für jeden Wert des Arguments X zu berechnen. Zum Beispiel berechnen wir für X=1 die Werte li(1) (i= 0,1,2,3):

l0(1)=0,7763; l1(1)= 3,5889; l2(1)=-1,5155;l3(1)=0,2966.

Summiert man die Werte von li(1) erhält man den Wert Yinterp(1)=3.1463.

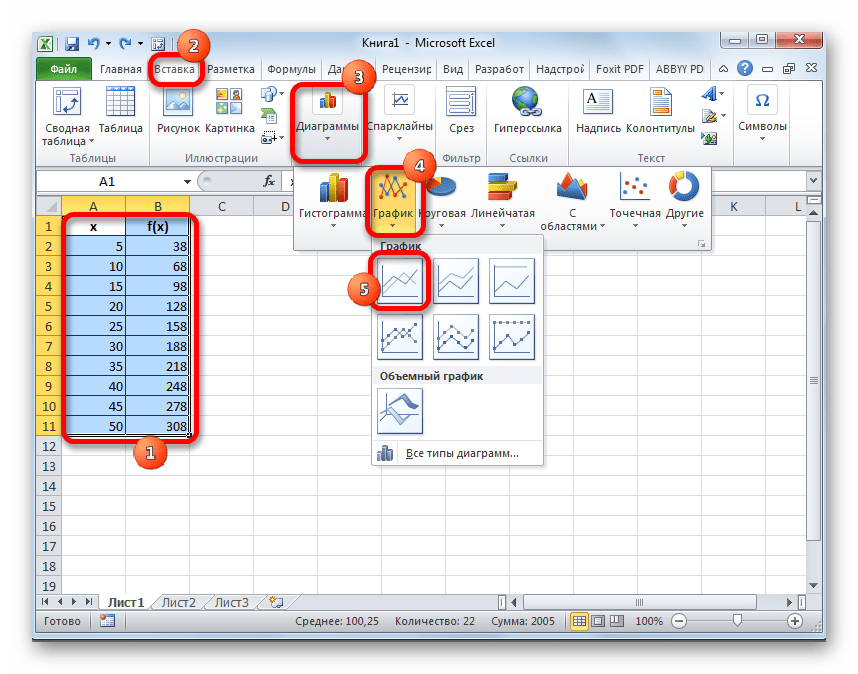
1.4.2. Implementierung des Interpolationsalgorithmus durch Lagrange-Formeln in der Umgebung des Programms Microsoft Excel

Die Implementierung des Interpolationsalgorithmus beginnt wie bei manuellen Berechnungen mit dem Schreiben von Formeln zur Berechnung der Koeffizienten qi. 9 zeigt die Spalten der Tabelle mit den gegebenen Werten des Arguments, der interpolierten Funktion und der Koeffizienten qi. Rechts von dieser Tabelle befinden sich die Formeln, die in die Zellen der Spalte C geschrieben werden, um die Werte der Koeffizienten qi zu berechnen.

ВС2: "=B2/((A2-A3)*(A2-A4)*(A2-A5))" Æ q0

c3: "=B3/((A3-A4)*(A3-A5)*(A3-A2))" Æ q1

c4: "=B4/((A4-A5)*(A4-A2)*(A4-A3))" Æ q2

vС5: "=B5/((A5-A2)*(A5-A3)*(A5-A4))" Æ q3

Reis. 9 Koeffiziententabelle qi und Berechnungsformeln

Nach Eingabe der Formel q0 in Zelle C2 wird diese durch die Zellen von C3 bis C5 gezogen. Danach werden die Formeln in diesen Zellen gemäß (16) auf die in Abb. 9.

Ycalc(xi),

Durch die Implementierung von Formeln (17) schreiben wir Formeln zur Berechnung der Werte li(x) (i=0,1,2,3) in die Zellen der Spalten D, E, F und G. In Zelle D2, um den Wert zu berechnen l0(x0), schreiben wir die Formel:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

wir erhalten die Werte l0 (xi) (i=0,1,2,3).

Das Verknüpfungsformat $A2 ermöglicht es Ihnen, die Formel entlang der Spalten E, F, G zu strecken, um Berechnungsformeln für die Berechnung von li(x0) (i=1,2,3) zu bilden. Das Ziehen einer Formel über eine Zeile ändert den Spaltenindex der Argumente nicht. Um li(x0) (i=1,2,3) nach dem Zeichnen der Formel l0(x0) zu berechnen, ist es notwendig, sie gemäß den Formeln (17) zu korrigieren.

In Spalte H tragen wir die Excel-Formeln zum Summieren von li(x) gemäß der Formel ein

(11) Algorithmus.

Auf Abb. 10 zeigt eine Tabelle, die in der Programmumgebung von Microsoft Excel implementiert ist. Ein Zeichen für die Richtigkeit der in die Zellen der Tabelle geschriebenen Formeln und der durchgeführten Rechenoperationen sind die resultierende Diagonalmatrix li(xj) (i=0,1,2,3),(j=0,1,2, 3), Wiederholung der in Abb. 8 und eine Spalte mit Werten, die mit den Werten der interpolierten Funktion in den Knoten der ursprünglichen Tabelle übereinstimmen.

Reis. 10. Wertetabelle li(xj) (j=0,1,2,3) und Ycalc(xj)

Um die Werte an einigen Zwischenpunkten zu berechnen, reicht es aus

Geben Sie in den Zellen der Spalte A ab Zelle A6 die Werte des Arguments X ein, für das Sie die Werte der interpolierten Funktion bestimmen möchten. Markieren

in der letzten (5.) Zeile der Zellentabelle von l0(xn) bis Ycalc(xn) und dehnen Sie die in den ausgewählten Zellen geschriebenen Formeln bis zur Zeile mit der letzten

der gegebene Wert des x-Arguments.

Auf Abb. 11 zeigt eine Tabelle, in der die Berechnung des Wertes der Funktion an drei Punkten: x = 1, x = 2 und x = 3. In die Tabelle wurde eine zusätzliche Spalte mit Zeilennummern der Quelldatentabelle eingefügt.

Reis. 11. Berechnung der Werte interpolierter Funktionen mit Lagrange-Formeln

Zur übersichtlicheren Anzeige der Interpolationsergebnisse erstellen wir eine Tabelle, die eine Spalte mit Werten des Arguments X in aufsteigender Reihenfolge, eine Spalte mit Anfangswerten der Funktion Y(X) und eine Spalte enthält

Sagen Sie mir, wie man die Interpolationsformel verwendet und welche zur Lösung von Problemen in der Thermodynamik (Wärmetechnik)

Iwan Schestakowitsch

Die einfachste, aber oft nicht ausreichend genaue Interpolation ist die lineare. Wenn Sie bereits zwei bekannte Punkte haben (X1 Y1) und (X2 Y2) und Sie die Y-Werte des Tages von einigen X finden müssen, die zwischen X1 und X2 liegen. Dann ist die Formel einfach.
Y \u003d (Y2-Y1) * (X-X1) / (X2-X1) + Y1
Übrigens funktioniert diese Formel auch für X-Werte außerhalb des X1..X2-Intervalls, aber dies wird bereits als Extropolation bezeichnet und ergibt in einem erheblichen Abstand von diesem Intervall einen sehr großen Fehler.
Es gibt viele andere Matten. Interpolationsmethoden - Ich rate Ihnen, das Lehrbuch zu lesen oder im Internet zu stöbern.
Die Methode der grafischen Interpolation ist auch nicht ausgeschlossen - zeichnen Sie manuell einen Graphen durch bekannte Punkte und finden Sie Y aus dem Graphen für das erforderliche X. ;)

Roman

Sie haben zwei Bedeutungen. Und ungefähr die Abhängigkeit (linear, quadratisch, ..)
Der Graph dieser Funktion verläuft durch Ihre beiden Punkte. Sie brauchen einen Wert irgendwo dazwischen. Nun, ausdrücken!
Zum Beispiel. In der Tabelle beträgt der Sättigungsdampfdruck bei einer Temperatur von 22 Grad 120.000 Pa und bei 26 124.000 Pa. Dann bei einer Temperatur von 23 Grad 121000 Pa.

Interpolation (Koordinaten)

Auf der Karte befindet sich ein Koordinatengitter (Bild).
Es hat einige bekannte Referenzpunkte (n>3) mit zwei x,y-Werte- Koordinaten in Pixeln und Koordinaten in Metern.
Es ist notwendig, Zwischenwerte von Koordinaten in Metern zu finden, wobei die Koordinaten in Pixeln bekannt sind.
Lineare Interpolation ist nicht geeignet - zu viel Fehler außerhalb der Linie.
So: (Xc - Koordinate in Metern mal x, Xp - Koordinate in Pixel mal x, Xc3 - gewünschter Wert mal x)
Xc3= (Xc1-Xc2)/(Xp1-Xp2)*(Xp3-Xp2)+Xc2
Yc3 = (Yc1-Yc2)/(Yp1-Yp2)*(Yp3-Yp2)+Yc2

Wie findet man die gleiche Formel zum Finden von Xc und Yc, wenn nicht zwei (wie hier), sondern N bekannte Referenzpunkte gegeben sind?

Joka fern lowd

Stimmen die Achsen der Koordinatensysteme in Pixel und Metern nach den geschriebenen Formeln überein?
Das heißt, Xp -> Xc wird unabhängig interpoliert und Yp -> Yc wird unabhängig interpoliert. Wenn nicht, müssen Sie die zweidimensionale Interpolation Xp,Yp->Xc und Xp,Yp->Yc verwenden, was die Aufgabe etwas komplizierter macht.
Ferner wird angenommen, dass die Koordinaten Xp und Xc durch eine gewisse Abhängigkeit miteinander in Beziehung stehen.
Wenn die Art der Abhängigkeit bekannt ist (oder angenommen wird, wir nehmen zum Beispiel an, dass Xc=a*Xp^2+b*Xp+c), dann können Sie die Parameter dieser Abhängigkeit erhalten (für die gegebene Abhängigkeit a , b, c) verwenden Regressionsanalyse(Methode der kleinsten Quadrate) . Wenn Sie bei dieser Methode eine bestimmte Abhängigkeit Xc(Xp) angeben, können Sie eine Formel für die Parameter der Abhängigkeit von den Referenzdaten erhalten. Dieses Verfahren erlaubt es insbesondere, eine lineare Beziehung zu finden, die am besten zu einem gegebenen Datensatz passt.
Nachteil: Bei dieser Methode können die aus den Daten der Xp-Passpunkte gewonnenen Xc-Koordinaten von den vorgegebenen abweichen. So verläuft beispielsweise die durch die Versuchspunkte gezogene Näherungsgerade nicht genau durch diese Punkte selbst.
Wenn eine exakte Übereinstimmung erforderlich ist und die Art der Abhängigkeit unbekannt ist, sollten Interpolationsverfahren verwendet werden. Am mathematisch einfachsten ist das Lagrange-Interpolationspolynom, das genau durch die Bezugspunkte geht. Aufgrund des hohen Grades dieses Polynoms bei große Zahlen Referenzpunkten und schlechter Interpolationsqualität sollte man besser darauf verzichten. Der Vorteil ist die relativ einfache Formel.
Es ist besser, Spline-Interpolation zu verwenden. Das Wesentliche dieses Verfahrens besteht darin, dass in jedem Abschnitt zwischen zwei benachbarten Punkten die untersuchte Abhängigkeit durch ein Polynom interpoliert wird und Glättebedingungen an den Verbindungspunkten zweier Intervalle geschrieben werden. Der Vorteil dieser Methode liegt in der Qualität der Interpolation. Nachteile - Es ist fast unmöglich, eine allgemeine Formel abzuleiten, Sie müssen die Koeffizienten des Polynoms in jedem Abschnitt algorithmisch finden. Ein weiterer Nachteil ist die Schwierigkeit der Verallgemeinerung auf 2D-Interpolation.

Viele von uns sind in verschiedenen Wissenschaften auf unverständliche Begriffe gestoßen. Aber es gibt nur sehr wenige Menschen, die keine Angst vor unverständlichen Wörtern haben, sondern sie im Gegenteil aufmuntern und sie zwingen, sich eingehender mit dem zu studierenden Thema zu befassen. Heute werden wir über so etwas wie Interpolation sprechen. Dies ist eine Methode zum Zeichnen von Diagrammen unter Verwendung bekannter Punkte, die es ermöglicht, ihr Verhalten in bestimmten Abschnitten der Kurve mit einem Minimum an Informationen über die Funktion vorherzusagen.

Bevor wir zum Wesen der Definition selbst übergehen und ausführlicher darüber berichten, lassen Sie uns ein wenig in die Geschichte eintauchen.

Geschichte

Interpolation ist seit der Antike bekannt. Dieses Phänomen verdankt seine Entwicklung jedoch mehreren der prominentesten Mathematiker der Vergangenheit: Newton, Leibniz und Gregory. Sie waren es, die dieses Konzept mit den damals verfügbaren fortschrittlicheren mathematischen Methoden entwickelten. Zuvor wurde natürlich Interpolation angewendet und in Berechnungen verwendet, aber sie taten dies auf völlig ungenaue Weise und erforderten eine große Anzahl Daten, um ein mehr oder weniger realitätsnahes Modell zu erstellen.

Heute können wir sogar wählen, welches der Interpolationsverfahren besser geeignet ist. Alles wird in eine Computersprache übersetzt, die das Verhalten einer Funktion in einem bestimmten Bereich, begrenzt durch bekannte Punkte, mit großer Genauigkeit vorhersagen kann.

Interpolation ist ein ziemlich enges Konzept, daher ist seine Geschichte nicht so reich an Fakten. Im nächsten Abschnitt werden wir verstehen, was Interpolation eigentlich ist und wie sie sich von ihrem Gegenteil – der Extrapolation – unterscheidet.

Was ist Interpolation?

Wie wir bereits gesagt haben, ist dies der allgemeine Name für Methoden, mit denen Sie einen Graphen nach Punkten zeichnen können. In der Schule geschieht dies hauptsächlich durch das Erstellen einer Tabelle, das Identifizieren von Punkten in einem Diagramm und vorbildlicher Aufbau Linien, die sie verbinden. Die letzte Aktion basiert auf Überlegungen zur Ähnlichkeit der untersuchten Funktion mit anderen, deren Art von Graphen wir kennen.

Es gibt jedoch andere, komplexere und präzisere Wege, um die Aufgabe des Plottens eines Punkt-für-Punkt-Plots zu erfüllen. Die Interpolation ist also eigentlich eine "Vorhersage" des Verhaltens einer Funktion in einem bestimmten Bereich, begrenzt durch bekannte Punkte.

Es gibt ein ähnliches Konzept, das mit demselben Bereich verbunden ist - Extrapolation. Es ist auch eine Vorhersage des Graphen einer Funktion, aber über die bekannten Punkte des Graphen hinaus. Bei diesem Verfahren wird anhand des Verhaltens einer Funktion über ein bekanntes Intervall eine Vorhersage getroffen und diese Funktion dann auch auf ein unbekanntes Intervall angewendet. Diese Methode ist sehr praktisch für praktische Anwendung und wird beispielsweise in der Wirtschaft aktiv eingesetzt, um Höhen und Tiefen des Marktes und die demografische Situation im Land vorherzusagen.

Aber wir sind vom eigentlichen Thema abgewichen. Im nächsten Abschnitt werden wir verstehen, was Interpolation ist und welche Formeln verwendet werden können, um diese Operation durchzuführen.

Arten der Interpolation

bei den meisten einfache Ansicht ist die Nächste-Nachbar-Interpolation. Mit dieser Methode erhalten wir einen sehr ungefähren Plot, der aus Rechtecken besteht. Wenn Sie mindestens einmal eine Erklärung der geometrischen Bedeutung des Integrals auf einem Graphen gesehen haben, dann werden Sie verstehen, was grafische Form spricht.

Darüber hinaus gibt es noch weitere Interpolationsverfahren. Die bekanntesten und beliebtesten sind mit Polynomen verbunden. Sie sind genauer und ermöglichen die Vorhersage des Verhaltens einer Funktion mit einem eher mageren Satz von Werten. Die erste Interpolationsmethode, die wir uns ansehen werden, ist die lineare Polynominterpolation. Dies ist die einfachste Methode aus dieser Kategorie, und sicherlich hat sie jeder von Ihnen in der Schule verwendet. Sein Wesen liegt in der Konstruktion von geraden Linien zwischen bekannten Punkten. Wie Sie wissen, verläuft eine einzelne Gerade durch zwei Punkte der Ebene, deren Gleichung anhand der Koordinaten dieser Punkte gefunden werden kann. Nachdem wir diese geraden Linien gebaut haben, erhalten wir einen gebrochenen Graphen, der zumindest die ungefähren Werte der Funktionen und in widerspiegelt allgemein gesagt entspricht der Realität. So funktioniert die lineare Interpolation.

Komplizierte Arten der Interpolation

Es gibt eine interessantere, aber gleichzeitig komplexere Art der Interpolation. Erfunden hat es der französische Mathematiker Joseph Louis Lagrange. Deshalb ist die Berechnung der Interpolation nach diesem Verfahren nach ihm benannt: Interpolation nach dem Lagrange-Verfahren. Der Clou dabei: Wird bei der im vorigen Absatz beschriebenen Methode nur mit einer linearen Funktion gerechnet, so werden bei der Lagrange-Entwicklung auch Polynome höheren Grades verwendet. Aber es ist nicht so einfach, die Interpolationsformeln selbst zu finden verschiedene Funktionen. Und je mehr Punkte bekannt sind, desto genauer ist die Interpolationsformel. Aber es gibt noch viele andere Methoden.

Es gibt auch eine perfektere und realitätsnähere Berechnungsmethode. Die darin verwendete Interpolationsformel ist eine Sammlung von Polynomen, deren Anwendung jeweils vom Abschnitt der Funktion abhängt. Dieses Verfahren wird als Spline-Funktion bezeichnet. Darüber hinaus gibt es auch Möglichkeiten, so etwas wie die Interpolation von Funktionen zweier Variablen zu tun. Hier gibt es nur zwei Methoden. Darunter sind bilineare oder doppelte Interpolation. Mit dieser Methode können Sie ganz einfach ein Diagramm anhand von Punkten erstellen dreidimensionaler Raum. Andere Methoden sind davon nicht betroffen. Im Allgemeinen ist Interpolation ein universeller Name für alle diese Methoden zum Zeichnen von Graphen, aber die Vielfalt der Möglichkeiten, auf die diese Aktion ausgeführt werden kann, zwingt sie dazu, sie in Abhängigkeit von der Art der Funktion, die dieser Aktion unterliegt, in Gruppen einzuteilen. Das heißt, die Interpolation, von der wir oben ein Beispiel betrachtet haben, bezieht sich auf direkte Verfahren. Es gibt auch eine umgekehrte Interpolation, die sich dadurch unterscheidet, dass Sie keine direkte, sondern eine berechnen können Umkehrfunktion(d.h. x von y). Wir werden die letzteren Optionen nicht in Betracht ziehen, da sie ziemlich schwierig sind und eine gute mathematische Wissensbasis erfordern.

Kommen wir zu einem der vielleicht wichtigsten Abschnitte. Daraus lernen wir, wie und wo die Methoden, die wir besprechen, im Leben angewendet werden.

Anwendung

Wie Sie wissen, ist die Mathematik die Königin der Wissenschaften. Auch wenn Sie in bestimmten Operationen zunächst keinen Sinn sehen, bedeutet dies daher nicht, dass sie nutzlos sind. Zum Beispiel scheint die Interpolation eine nutzlose Sache zu sein, mit deren Hilfe nur Graphen erstellt werden können, die nur wenige Menschen jetzt brauchen. Bei allen Berechnungen in Ingenieurwissenschaften, Physik und vielen anderen Wissenschaften (z. B. Biologie) ist es jedoch äußerst wichtig, ein ziemlich vollständiges Bild des Phänomens zu präsentieren und gleichzeitig einen bestimmten Satz von Werten zu haben. Die über den Graphen verstreuten Werte selbst geben nicht immer eine klare Vorstellung vom Verhalten der Funktion in einem bestimmten Bereich, den Werten ihrer Ableitungen und den Schnittpunkten mit den Achsen. Und das ist für viele Bereiche unseres Lebens sehr wichtig.

Und wie wird es im Leben nützlich sein?

Es kann sehr schwierig sein, eine solche Frage zu beantworten. Aber die Antwort ist einfach: Auf keinen Fall. Dieses Wissen nützt Ihnen nichts. Aber wenn Sie dieses Material und die Methoden verstehen, mit denen diese Aktionen ausgeführt werden, werden Sie Ihre Logik trainieren, was im Leben sehr nützlich sein wird. Entscheidend ist nicht das Wissen an sich, sondern die Fähigkeiten, die man sich im Studium aneignet. Schließlich gibt es nicht umsonst ein Sprichwort: „Ein Jahrhundert leben – ein Jahrhundert lernen“.

Verwandte konzepte

Wie wichtig dieser Bereich der Mathematik war (und immer noch ist), können Sie selbst nachvollziehen, wenn Sie sich die Vielfalt anderer damit verbundener Konzepte ansehen. Wir haben bereits über Extrapolation gesprochen, aber es gibt auch eine Annäherung. Vielleicht haben Sie dieses Wort schon einmal gehört. Was das bedeutet, haben wir in diesem Artikel jedenfalls auch analysiert. Approximation, wie Interpolation, sind Konzepte, die sich auf das Zeichnen von Funktionsgraphen beziehen. Der Unterschied zwischen dem ersten und dem zweiten besteht jedoch darin, dass es sich um eine ungefähre Konstruktion eines Graphen handelt, der auf ähnlichen bekannten Graphen basiert. Diese beiden Konzepte sind einander sehr ähnlich und umso interessanter ist es, sie zu studieren.

Fazit

Mathematik ist keine so schwierige Wissenschaft, wie es auf den ersten Blick scheint. Sie ist ziemlich interessant. Und in diesem Artikel haben wir versucht, es Ihnen zu beweisen. Wir haben uns die Konzepte angesehen, die mit dem Zeichnen von Diagrammen verbunden sind, haben gelernt, was doppelte Interpolation ist, und anhand von Beispielen analysiert, wo sie verwendet wird.

Es gibt Fälle, in denen es erforderlich ist, die Ergebnisse der Auswertung einer Funktion außerhalb des bekannten Bereichs zu kennen. Diese Problematik ist insbesondere für das Prognoseverfahren relevant. Excel hat mehrere Möglichkeiten, dies zu tun. Betrachten wir sie anhand konkreter Beispiele.

Methode 2: Extrapolation für den Graphen

Sie können das Extrapolationsverfahren für ein Diagramm durchführen, indem Sie eine Trendlinie zeichnen.

1. Zunächst erstellen wir das Diagramm selbst. Wählen Sie dazu mit dem Cursor bei gedrückter linker Maustaste den gesamten Bereich der Tabelle aus, inklusive der Argumente und der dazugehörigen Werte der Funktion. Wechseln Sie dann zur Registerkarte "Einfügung", klicken Sie auf die Schaltfläche "Zeitlicher Ablauf". Dieses Symbol befindet sich im Block "Diagramme" auf der Symbolleiste. Es erscheint eine Liste Verfügbare Optionen Grafiken. Wir wählen nach unserem Ermessen die geeignetsten aus.



2. Nachdem das Diagramm erstellt wurde, entfernen Sie die zusätzliche Zeile des Arguments, indem Sie es auswählen und auf die Schaltfläche klicken Löschen auf einer Computertastatur.



3. Als nächstes müssen wir die Unterteilungen der horizontalen Skala ändern, da sie die Werte der Argumente nicht so anzeigt, wie wir es brauchen. Klicken Sie dazu mit der rechten Maustaste auf das Diagramm und halten Sie in der erscheinenden Liste bei dem Wert an "Daten auswählen".



4. Klicken Sie im geöffneten Datenquellen-Auswahlfenster auf die Schaltfläche "Veränderung" im Block zum Bearbeiten der Beschriftung der horizontalen Achse.



5. Das Fenster zur Einstellung der Achsenbeschriftung wird geöffnet. Wir setzen den Cursor in das Feld dieses Fensters und wählen dann alle Daten in der Spalte aus "X" ohne seinen Namen. Klicken Sie dann auf die Schaltfläche OK.



6. Wiederholen Sie nach der Rückkehr zum Fenster zur Auswahl der Datenquelle denselben Vorgang, dh klicken Sie auf die Schaltfläche OK.



7. Jetzt ist unser Chart vorbereitet und Sie können direkt mit dem Aufbau einer Trendlinie beginnen. Wir klicken auf das Diagramm, woraufhin ein zusätzlicher Satz Registerkarten in der Multifunktionsleiste aktiviert wird - „Arbeiten mit Diagrammen“. Wechseln zur Registerkarte "Layout" und klicken Sie auf die Schaltfläche "Trendlinie" im Block "Analyse". Klicken Sie auf einen Artikel "Lineare Näherung" oder "Exponentiale Annäherung".



8. Die Trendlinie wird hinzugefügt, befindet sich jedoch vollständig unter der Linie des Diagramms selbst, da wir den Wert des Arguments, nach dem sie streben soll, nicht angegeben haben. Klicken Sie dazu erneut auf die Schaltfläche "Trendlinie", aber wählen Sie jetzt das Element aus "Erweiterte Trendlinienoptionen".



9. Das Fenster „Trendline-Format“ wird geöffnet. Im Kapitel "Trendlinienoptionen" Es gibt einen Einstellungsblock "Vorhersage". Nehmen wir wie bei der vorherigen Methode das Argument für die Extrapolation 55 . Wie Sie sehen können, hat der Graph bisher eine Länge bis zum Argument 50 inklusive. Es stellt sich heraus, dass wir es um ein weiteres verlängern müssen 5 Einheiten. Auf der horizontalen Achse können Sie sehen, dass 5 Einheiten einer Division entsprechen. Das ist also eine Periode. Auf dem Feld "Weitermachen mit" geben Sie den Wert ein "eines". Klicken Sie auf die Schaltfläche "Nah dran" in der unteren rechten Ecke des Fensters.



10. Wie Sie sehen können, wurde der Chart anhand der Trendlinie um die angegebene Länge verlängert.

Daher haben wir die einfachsten Beispiele für die Extrapolation von Tabellen und Grafiken betrachtet. Im ersten Fall wird die Funktion verwendet VORHERSAGE, und im zweiten - die Trendlinie. Anhand dieser Beispiele lassen sich aber auch wesentlich komplexere Prognoseprobleme lösen.

Interpolation. Einführung. Allgemeine Problemstellung

Bei der Lösung verschiedener praktischer Probleme werden die Forschungsergebnisse in Form von Tabellen erstellt, die die Abhängigkeit einer oder mehrerer gemessener Größen von einem bestimmenden Parameter (Argument) zeigen. Solche Tabellen werden normalerweise in Form von zwei oder mehr Zeilen (Spalten) dargestellt und zur Bildung mathematischer Modelle verwendet.

Funktionen, die in mathematischen Modellen in Tabellen angegeben sind, werden normalerweise in Tabellen der Form geschrieben:

Y1(X)	Y(X0)	Y(X1)		Y(Xn)
Ym(X)	Y(X0)	Y(X1)		Y(Xn)

Die begrenzte Information, die solche Tabellen liefern, erfordert in einigen Fällen, die Werte der Funktionen Y j (X) (j=1,2,…,m) an Punkten X zu erhalten, die nicht mit den Knotenpunkten der Tabelle übereinstimmen X ich (i=0,1,2,… ,n). In solchen Fällen ist es notwendig, einen analytischen Ausdruck φ j (X) zu bestimmen, um die Näherungswerte der untersuchten Funktion Y j (X) an willkürlich festgelegten Punkten X zu berechnen. Die Funktion φ j (X), die zur Bestimmung der Näherungswerte der Funktion Y j (X) verwendet wird, wird als Näherungsfunktion bezeichnet (vom lateinischen approximo - Annäherung). Die Nähe der Näherungsfunktion ϕ j (X) zur Näherungsfunktion Y j (X) wird durch die Wahl des geeigneten Näherungsalgorithmus sichergestellt.

Alle weiteren Überlegungen und Schlussfolgerungen werden wir für Tabellen anstellen, die die Anfangsdaten einer untersuchten Funktion enthalten (also für Tabellen mit m=1 ).

1. Methoden der Interpolation

1.1 Darstellung des Interpolationsproblems

Meistens wird zur Bestimmung der Funktion φ(X) eine Aussage verwendet, die als Aussage des Interpolationsproblems bezeichnet wird.

Bei dieser klassischen Formulierung des Interpolationsproblems ist es erforderlich, eine näherungsweise analytische Funktion φ(X) zu bestimmen, deren Werte an den Knotenpunkten X i den Werten entsprechen Y(X i ) der Originaltabelle, d.h. Bedingungen

ϕ (X ich )= Y ich (ich = 0,1,2,...,n )

Die so konstruierte Näherungsfunktion φ(X) ermöglicht es, innerhalb des Wertebereichs des Arguments [X 0 ; X n ], definiert durch die Tabelle. Wenn Sie die Werte des X-Arguments festlegen, nicht besessen In diesem Intervall wird die Interpolationsaufgabe in die Extrapolationsaufgabe umgewandelt. In diesen Fällen die Genauigkeit

Werte, die bei der Berechnung der Werte der Funktion φ(X) erhalten werden, hängen vom Abstand des Werts des Arguments X von X 0 ab, wenn X<Х 0 , или отХ n , еслиХ >Xn.

Bei mathematische Modellierung die Interpolationsfunktion kann verwendet werden, um die Näherungswerte der zu untersuchenden Funktion an Zwischenpunkten der Teilintervalle [Х i ; Xi+1]. Ein solches Verfahren wird aufgerufen Tischsiegel.

Der Interpolationsalgorithmus wird durch die Methode zur Berechnung der Werte der Funktion φ(X) bestimmt. Die einfachste und naheliegendste Implementierung der Interpolationsfunktion besteht darin, die untersuchte Funktion Y(X) auf dem Intervall [X i ; Х i+1 ] durch ein Liniensegment, das die Punkte Y i , Y i+1 verbindet. Dieses Verfahren wird als lineares Interpolationsverfahren bezeichnet.

1.2 Lineare Interpolation

Bei der linearen Interpolation wird der Wert der Funktion am Punkt X, der sich zwischen den Knoten X i und X i+1 befindet, durch die Formel einer geraden Linie bestimmt, die zwei benachbarte Punkte der Tabelle verbindet

Y(X) = Y(Xi)+	Y(Xi + 1 ) − Y(Xi )	(X − Xi ) (i= 0,1,2, ...,n),
	Xi+ 1− Xi

Auf Abb. 1 zeigt ein Beispiel einer Tabelle, die als Ergebnis von Messungen eines bestimmten Werts Y(X) erhalten wird. Zeilen der Quelltabelle sind hervorgehoben. Rechts neben der Tabelle befindet sich ein Streudiagramm, das dieser Tabelle entspricht. Die Verdichtung der Tabelle erfolgt aufgrund der Berechnung nach der Formel

(3) Werte der Funktion, die an den Punkten Х angenähert werden, die den Mittelpunkten der Teilintervalle entsprechen (i=0, 1, 2, … , n ).

Abb.1. Komprimierte Tabelle der Funktion Y(X) und ihr entsprechendes Diagramm

Betrachtet man den Graphen in Abb. Aus 1 ist ersichtlich, dass die Punkte, die als Ergebnis der Komprimierung der Tabelle unter Verwendung des linearen Interpolationsverfahrens erhalten wurden, auf den Liniensegmenten liegen, die die Punkte der ursprünglichen Tabelle verbinden. Lineare Genauigkeit

Interpolation, hängt im Wesentlichen von der Art der interpolierten Funktion und vom Abstand zwischen den Knoten der Tabelle X i, , X i+1 ab.

Offensichtlich, wenn die Funktion reibungslos ist, dann sogar für relativ Fern zwischen den Knoten ermöglicht ein Graph, der durch Verbinden der Punkte mit geraden Liniensegmenten konstruiert wird, eine genaue Abschätzung der Natur der Funktion Y(X). Wenn sich die Funktion schnell genug ändert und die Abstände zwischen den Knoten groß sind, erlaubt die lineare Interpolationsfunktion keine ausreichend genaue Annäherung an die reale Funktion.

Die lineare Interpolationsfunktion kann für eine allgemeine vorläufige Analyse und Bewertung der Korrektheit der Interpolationsergebnisse verwendet werden, die dann durch andere genauere Verfahren erhalten werden. Eine solche Bewertung wird besonders relevant in Fällen, in denen Berechnungen manuell durchgeführt werden.

1.3 Interpolation durch kanonisches Polynom

Das Verfahren zum Interpolieren einer Funktion durch ein kanonisches Polynom basiert auf dem Konstruieren einer Interpolationsfunktion als Polynom in der Form [ 1 ]

ϕ (x) = Pn (x) = c0 + c1 x + c2 x2 + ... + cn xn

Die Koeffizienten mit i des Polynoms (4) sind freie Interpolationsparameter, die aus den Lagrange-Bedingungen bestimmt werden:

Pn (xi )= Yi , (i= 0 , 1 , ... , n)

Mit (4) und (5) schreiben wir das Gleichungssystem

	Cx+ cx2				Cxn = Y
	Cx+ cx2				Cxn
			Cx2			Cxn = Y

Der Lösungsvektor mit i (i = 0, 1, 2, …, n ) des linearen algebraischen Gleichungssystems (6) existiert und kann gefunden werden, wenn es unter den i Knoten keine passenden Knoten gibt. Die Determinante von System (6) wird Vandermonde-Determinante1 genannt und hat einen analytischen Ausdruck [2].

1 Vandermondes Determinante Determinante genannt

Sie ist genau dann Null, wenn für einige xi = xj ist. (Material aus Wikipedia - der freien Enzyklopädie)

Um die Werte der Koeffizienten mit i zu bestimmen (i = 0, 1, 2, … , n)

Gleichungen (5) können in Vektormatrixform geschrieben werden

A*C=Y,

wobei A die Koeffizientenmatrix ist, bestimmt durch die Potenztabelle des Argumentvektors X= (x i 0 , x i , x i 2 , … , x i n ) T (i = 0, 1, 2, … , n)

				x0 2		x0 n
				x 2		xn n

C ist ein Spaltenvektor von Koeffizienten i (i = 0, 1, 2, …, n), und Y ist ein Spaltenvektor von Werten Y i (i = 0, 1, 2, …, n) des Interpolierten Funktion an den Stützstellen.

Die Lösung dieses Systems linearer algebraischer Gleichungen kann durch eine der in [3] beschriebenen Methoden erhalten werden. Zum Beispiel nach der Formel

Ñ ​​= A− 1 Y,

wobei A -1 die inverse Matrix von Matrix A ist. Um die inverse Matrix A -1 zu erhalten, können Sie die Funktion INV() verwenden, die im Satz von Standardfunktionen des Programms Microsoft Excel enthalten ist.

Nachdem die Werte der Koeffizienten mit i bestimmt wurden, können mit der Funktion (4) die Werte der interpolierten Funktion für jeden Wert der Argumente berechnet werden.

Lassen Sie uns die Matrix A für die in Abb. 1 gezeigte Tabelle schreiben, ohne die Zeilen zu berücksichtigen, die die Tabelle verdichten.

Abb.2 Matrix des Gleichungssystems zur Berechnung der Koeffizienten des kanonischen Polynoms

Unter Verwendung der Funktion MOBR() erhalten wir die Matrix A -1 invers zu Matrix A (Fig. 3). Dann erhalten wir gemäß Formel (9) den in Abb. 1 gezeigten Koeffizientenvektor С=(c 0 , c 1 , c 2 , …, c n ) T. vier.

Um die Werte des kanonischen Polynoms in der Zelle der Spalte Y kanonisch zu berechnen, die den Werten 0 entspricht, führen wir die in die folgende Form umgewandelte Formel ein, die der Nullzeile des Systems entspricht (6)

=((((c 5	* x 0 + c 4 ) * x 0 + c 3 ) * x 0 + c 2 ) * x 0 + c 1 ) * x 0 + c 0

C0 +x *(c1 + x *(c2 + x*(c3 + x*(c4 + x* c5 ))))

Statt „ c i “ in die in die Zelle der Excel-Tabelle eingetragene Formel zu schreiben, sollte ein absoluter Bezug auf die entsprechende Zelle stehen, die diesen Koeffizienten enthält (siehe Abb. 4). Anstelle von "x 0" - ein relativer Verweis auf die Spalte Spalte X (siehe Abb. 5).

Y kanonisch (0) des Werts, der mit dem Wert in Zelle Y lin (0) übereinstimmt. Beim Ziehen einer Formel, die in eine Zelle Y kanonisch (0) geschrieben wurde, müssen die Werte von Y kanonisch (i) ebenfalls übereinstimmen, entsprechend den Knotenpunkten des Originals

Tabellen (siehe Abb. 5).

Reis. 5. Diagramme, die nach den Tabellen der linearen und kanonischen Interpolation erstellt wurden

Beim Vergleich von Graphen von Funktionen, die nach Tabellen erstellt wurden, die mit den Formeln der linearen und kanonischen Interpolation berechnet wurden, sehen wir in einer Reihe von Zwischenknoten eine signifikante Abweichung der Werte, die durch die Formeln der linearen und kanonischen Interpolation erhalten wurden. Es ist vernünftiger, die Genauigkeit der Interpolation basierend auf dem Erhalt zusätzlicher Informationen über die Natur des zu modellierenden Prozesses zu beurteilen.